Objectives
We seek
to evaluate the accuracy of computational intelligence (CI)
methods in time series forecasting, extending the earlier
NN3 & NN5 competitions unto a new set of data of multiple
frequencies.
We seek to
determine progress in modelling CI for forecasting & to disseminate
knowledge on “best practices” across time series of different frequencies. To
facilitate and knowledge exchange, the competition will be
run in 3 separate tournaments of 6 months each. In each
tournament one, two or more of the 6 datasets of 11 time
series each with a particular time frequency must be
forecasted. To extend the task across the year, the datasets
in each tournament round will be released sequentially 2 at
a time. The contestants will use a consistent methodology
within each tournament, but will be allowed to change their
methodology between tournaments.
Previous Runs
We have launched the competition
after a trial run on a subset of time series and data
frequencies at 2009 IJCNN. No test data has ever been
disclosed.
Methods
The prediction competition is open to all methods of computational
intelligence, incl. feed-forward and recurrent neural networks,
fuzzy predictors, evolutionary & genetic algorithms, decision & regression tress, support vector
regression, hybrid approaches etc. used in all areas of forecasting,
prediction & time series analysis. We also welcome
submission of statistical methods as benchmarks, but they
are not eligible to "win" the NN GC.
Dissemination &
Publication
of Results
All those submitting predictions will be invited to
participate in sessions at the 2010 International Joint Conference
of Neural Networks IJCNN, Barcelona, Spain and addition
conferences to be announced soon. Each workshop will provide awards by dataset for students and non-students.
We are currently not seeking for a journal special issue for accepted submissions,
but this may follow in the next year.
Acknowledgement
Thanks to Isabelle Guyon,
Clopinet USA, for her idea of conducting a 'Grand Challenge'
of a competition - this is not it, but it aims to extend the
reliability of results beyond those competitions run
before. Also thanks to other researchers for the idea
of conducting multiple small staged competition runs similar
to a sports tournament.
Disclaimer
The competition is conducted
purely for academic purposes
and should not be exploited commercially. |
 Forecasting
Problem Forecasting
Problem
Forecast
one, two or more datasets of a selection of 6 datasets (each
containing 11 time series)
on
transportation data
as accurately as possible, using methods from computational intelligence and
applying a consistent methodology.
The data consists
of 6 datasets with 11 time series with different
time frequencies, including yearly, quarterly, monthly,
weekly, daily and hourly transportation data (see series examples
in that order below) :
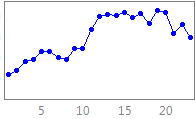 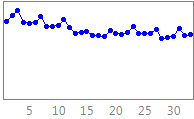
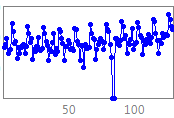 
 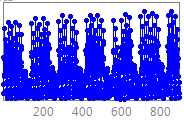
Transportation is considered as a prerequisite to economy
prosperity, mobility and wellbeing in a civilised world, in
addition to providing one of the largest service sectors
worldwide. Forecasting time series of transportation demand and flows,
including airline, rail and car passenger traffic, provides
a number of challenges: data may be measured at different time frequencies.
Depending on the time frequency, the data may contain
a number of time series patterns including none to multiple
overlying seasonality, local trends, structural breaks,
outliers, zero and missing values etc. These are often
driven by a combination of unknown and unobserved causal
forces driven by the underlying yearly calendar, such as
reoccurring seasonal periods, bank holidays, or special
events of different length and magnitude of impact, with
different lead and lag effects.
|











